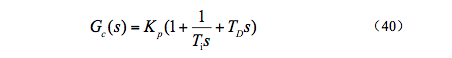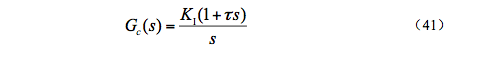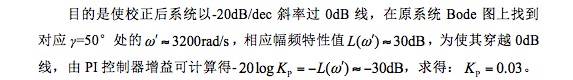4.4 Buck變換器的(de)PI控制器頻(pín)域設計方法
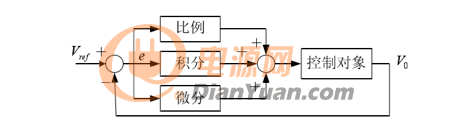
實際應用(yòng)中,最廣泛的(de)控制器爲比例(P),積分(fēn)(I),微分(fēn)(D)控制,簡稱PID控制。這(zhè)是一種線性控制方法,它通(tōng)過設定值和(hé)實際值産生偏差,将偏差的(de)比例、積分(fēn)、微分(fēn)通(tōng)過線性組合構成控制量,對(duì)被控對(duì)象進行控制。
圖15 PID控制器原理(lǐ)圖
其傳遞函數可(kě)表示爲:
在上式中,Ti爲積分(fēn)時(shí)間常數,TD爲微分(fēn)時(shí)間常數。
在比例,積分(fēn),微分(fēn)三個(gè)控制因子中,比例控制能迅速反應誤差,但比例控制不能消除穩态誤差,且比例系數的(de)增大(dà)會引起系統不穩定;積分(fēn)控制的(de)作用(yòng)是:隻要系統存在誤差,積分(fēn)控制作用(yòng)就不斷的(de)積累,輸出控制量控制誤差,故隻要有足夠的(de)時(shí)間,積分(fēn)控制就能完全消除誤差,積分(fēn)作用(yòng)太強會使系統超調加大(dà),甚至使系統出現振蕩;微分(fēn)控制可(kě)以反映偏差信号的(de)變化(huà)趨勢,減小超調量,克服振蕩,使系統的(de)穩定性提高(gāo),同時(shí)加快(kuài)系統的(de)動态響應速度,減小調整時(shí)間,從而改善系統動态性能。實際控制過程中,往往根據系統性能指标的(de)要求采用(yòng)不同的(de)組合校正方式,如PI、PD、PID等。
對(duì)于Buck變換器采用(yòng)PI控制,從頻(pín)率特性角度看PI控制實質上相當于滞後校正。由式(44),令TD=0,可(kě)得(de)典型PI調節器的(de)傳遞函數爲
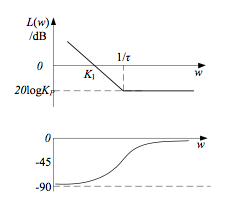
式中 , ,PI控制器的(de)對(duì)數頻(pín)率特性曲線如圖16所示
圖16 PI控制器幅頻(pín)特性曲線
轉折頻(pín)率爲 ,增益爲-20logKP。因爲PI控制器作用(yòng)原理(lǐ)相當于滞後校正,參數設計可(kě)按串聯滞後環節原則确定。在上一小節原系統Bode圖分(fēn)析中可(kě)知,高(gāo)頻(pín)段以斜率爲-40dB/dec穿越0dB線,且相角裕量Pm≈4°。加入PI校正環節之後,目的(de)是要增大(dà)相角裕量,校正環節的(de)轉折頻(pín)率 使校正後的(de)系統具有新的(de)截止頻(pín)率,并且以-20dB/dec斜率過0dB線。按照(zhào)以下(xià)步驟設計PI控制器參數。
(1)确定校正後系統相角裕量;
按穩定系統相角裕量爲45°的(de)原則,并考慮留有一定裕量,取γ=50°,使校正後系統相角裕量約爲50°。
(2)确定PI控制器參數 ;
(3)确定PI控制器參數K1 ;
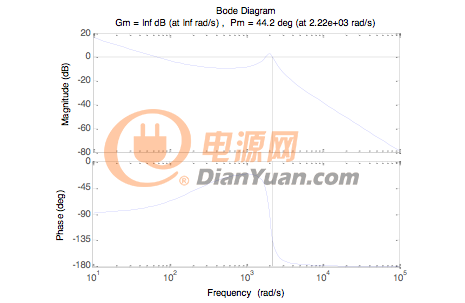
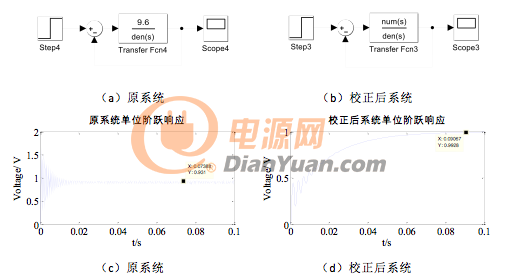
校正後系統的(de)Bode圖如圖17所示爲,可(kě)以看出相角裕度爲44.2°滿足要求。爲了(le)對(duì)比PI控制器對(duì)Buck變換器的(de)控制效果,以下(xià)分(fēn)别觀察原系統和(hé)加PI控制器校正後系統的(de)單位階躍響應,Matlab/Simulink仿真模型如圖18(a)(b)所示,單位階躍響應如圖18(c)(d)所示。可(kě)以看出原系統是穩定的(de),但存在較大(dà)的(de)輸出超調,且一直處于振蕩狀态,且輸出平均值小于設定值1,存在誤差;而校正後的(de)系統無超調且振蕩減少,穩定後,值爲1,但是有較長(cháng)的(de)調節時(shí)間,主要是由于PI參數還(hái)未達最優值,需要進一步調節PI參數。另外一個(gè)原因是由于PI控制器本身就是一個(gè)滞後環節,通(tōng)過犧牲系統的(de)快(kuài)速性而獲得(de)高(gāo)的(de)穩态性能。
圖17 校正後系統Bode圖
圖18 單位階躍響應仿真框圖及結果